Cyclomatic Complexity serves as a fundamental metric of code complexity and has well known usage in software testing and analyis. While it’s built on a sound and interesting graph-theory concept, it has fair share of problems associated with it.
What is Cyclomatic Complexity ?
Definition
Cyclomatic complexity represents the number of linearly independent paths possible in the code. In other words, it symbolises the number of branching existing in the code.
The intent of this number is to capture the amount of decision logic being performed in the concerned piece of code.
A bit of a history …
Interestingly, this metric was introduced by Thomas McCabe in 1976 at a theoretical level aiming to measure the structured complexity of programs in a quantitative way during that time. However, even though it might seem that this metric has an old history , it still is relevant and heavily influential in today’s software discussions.
FYI, i like abbreviations :)
What is it computed for ?
The original publication by McCabe, referred to the concept of CC to be computed for a ‘module’. It could resemble to a function or a method in modern programming languages. I’ll talk about how a granular level complexity check is beneficial.
How is it computed ?
CC is calculated through the program’s control-flow graph, where nodes represent cohesive sets of commands (called as a block) , and directed edges link nodes if the execution of the second command is a potential immediate follow-up to the first one.
Here, a conditional or loop or similar statements (represented as nodes) would have multiple branching (multiple out-edges) which is used in computation the CC number.
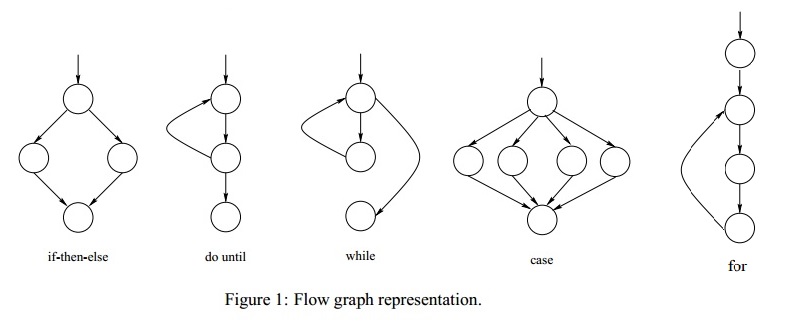
Mathematical Foundation
Graph Theory
Cyclomatic number is a value in graph theory that tells you the number of the edges required to be remove and break all cycles of the graph i.e the number of independent paths in a graph. Note that its only valid for for strongly connected graphs. It is also known as a ‘circuit rank’ and has quite diverse use cases beyond this software analysis.
The cyclomatic number can be derived by :
\[rank = E - N + C\]Here, E represents the number of edges, N represents the number of nodes and C represents the connected components. The derivation of this formula is based on the manipulation of famous Kirchhoff’s Law from the Linear Algebra.
McCabe’s derivation
Program control flow graphs do not inherently exhibit strong connectivity. However, the introduction of a “virtual edge” that connects the exit node to the entry node transforms them into strongly connected graphs. The definition of cyclomatic complexity for program control flow graphs is derived from the cyclomatic number formula by a straightforward addition of one, signifying the impact of the virtual edge. This interpretation aligns cyclomatic complexity with the count of independent paths within the standard control flow graph model, elegantly sidestepping the need for explicit reference to the virtual edge. Since for CFGs, the connected component is 1 as we are considering a single function or method. This gives us :
\[cc = E - N + 1\]Taking into consideration the virtual edge - which inevidently contributes to the branching count , the formula becomes :
\[cc = E - N + 2\]McCabe proposed a generic formula for “P” number of program exits (was common in the older era program with goto statements)
\[cc = E - N + 2P\]Intuitive understanding
Let’s break up the CC formula to 3 segments :
\(cc = E - N + 2\) \(\) \(cc = (E - N) + (1) + (1)\)
E-Nwould nullify all the nodes with 1 branch and will render us with the count of extra branches of the nodes,1is added for considering the default path (no branch diversion)1is accounting for the ‘virtual edge’ added for the mathematical convenience
Examples of code snippets and associated CC
I have included some function snippets below. Guess the complexity of these functions and verify them in the table at the end of the section.
void foo0( int a ) {
a--;
return ;
}
void foo1( int a ) {
if ( a )
return ;
else
return ;
}
void foo2( int a ) {
if ( a )
return ;
}
void foo3( int a, int b ) {
if ( a && b )
return ;
}
void foo4( int a, int b ) {
if ( a )
return ;
if ( b )
return ;
}
void foo5( int a, int b ) {
if ( a )
if ( b )
return ;
}
void foo6( int a ) {
while ( a )
a-- ;
}
void foo7( int a ) {
do
a-- ;
while ( a );
}
void foo8( int a ) {
for ( int x = 0; x < a; x++ )
foo() ;
}
void foo9( int a ) {
switch ( a )
{
case 1:
return ;
}
}
void foo10( int a ) {
switch ( a )
{
case 1:
case 2:
return ;
}
}
| Function name | Cyclomatic Complexity |
|---|---|
| foo0 | 1 |
| foo1 | 2 |
| foo2 | 2 |
| foo3 | 2 |
| foo4 | 3 |
| foo5 | 3 |
| foo6 | 2 |
| foo7 | 2 |
| foo8 | 2 |
| foo9 | 2 |
| foo10 | 3 |
How does it help in software development and processes ?
Source-Code Quality effects
Error Proneness: - Overly complex modules are more susceptible to errors. - High cyclomatic complexity increases the likelihood of introducing bugs.
Code Understandability and Modularity: - Complex modules are less modular, harder to understand, leading to challenges in comprehension. - Lower cyclomatic complexity promotes code readability and ease of understanding.
Maintainability: - Modifying highly complex code becomes a daunting task. - Lower cyclomatic complexity supports easier and safer code modifications.
Assessment of undiscovered Bugs: - Cyclomatic complexity serves as an indicator of the risk that a function contains undiscovered bugs.
Modification Risk: - It assesses the risk associated with modifying a function, gauging the potential injection of bugs or the difficulty of additions.
Wider infrastructural effects
Testing infrastructure effects: - Testing complex modules is inherently more challenging. - Lower cyclomatic complexity facilitates more effective and comprehensive testing.
Departmental Standards: - Deliberate limits on complexity, established as departmental standards, foster software quality. - Organizations benefit from avoiding pitfalls associated with high complexity software.
Operational Advantages: - Projects with operational advantages, such as experienced staff, formal design, modern programming language, structured programming, code walkthroughs, and comprehensive test plans, can consider higher complexity limits.
Complexity Considerations

Optimal Complexity Limit: - The optimal complexity limit remains somewhat controversial. - McCabe’s original limit of 10 has significant supporting evidence. - Successful use of limits exceeding 10 has been observed, reaching up to 15.
Project-Specific Considerations: - Limits above 10 should be reserved for projects with operational advantages. - These include experienced staff, formal design, a modern programming language, structured programming, code walkthroughs, and a comprehensive test plan.
Testing Effort: - Organizations can choose a complexity limit greater than 10 but must be aware of the additional testing effort required for more complex modules. - Requires a clear understanding and willingness to devote resources to thorough testing.
Interesting use cases that I worked for
Gray box testing
Previously, while working in the field of clone detection and semantic code search - I got involved in employing gray-box testing to evaluate if a pair of code is similar or not (semantically). The accuracy and precision of this approach solely dependent on the coverage or effectiveness of the gray-box testing. The effectiveness of gray-box testing was improved by the usage of cyclomatic complexity.
Gray-box testers can use cyclomatic complexity to identify critical paths and decision points within the code. It helps a lot in designing test cases that cover different paths through the code.
Network routing mechanisms
A graph characterized by a cyclomatic number (or circuit rank) r is often referred to as an r-almost-tree. This nomenclature stems from the property that merely r edges need removal to transform the graph into a tree or a forest. Specifically, a 1-almost-tree is termed a near-tree. In the context of connected near-trees, they manifest as pseudotrees—cycles wherein each vertex is associated with a (potentially trivial) tree rooted at that vertex.
In one of my failed experiments, we tried solving a NS2 network simulation problem , where we had to efficient manage a network traffic with appropriate load balancing algorithms. One of the approaches, that were tried out was to find out if we could convert the existing graph into tree and use better and famous tree based routing systems. The circuit rank gives us an interesting estimate on the property of the graph and how we can leverage it for tree conversion.
How to use it with tools ?
There are multiple category of tools that do the CC checks for you. Many these tools easily get integrated with your CI/CD pipeline.
- IDE integrated CC checkers :
- Visual Studio built-in functionality for cyclomatic complexity out-of-the-box.
- Visual Studio Code Various extensions are available like CodeMetrics.
- JetBrains ReSharper
- CodeRush
- Eclipse Metric Plugin
- Linter based checkers :
- ESLint
- JSHint
- PyLint
- The OGs :
Breaking the system
The most interesting question of them all is to explore what reduces the CC number afterall ? There are multiple hacks around it and some better coding designs as well. Here we will be exploring some of them :
Long boolean expression
- Multiple operators in a single if condition.
int foo (int a, int b) { if (a > 17 && b < 42 && a + b < 55) { return 1; } return 2; } - Such code snippets are still generally considered of lower complexity (in this case of 2)
- Many people prefer this way of concatenating conditions instead of writing down nested if conditions.
- Although its a subjective call, but from testing p.o.v - this code snippet still requires to be tested over atleast 4 decision scenarios.
- Different tools report different results here : Complexity 2 by the Eclipse Metrics Plugin, with 4 by GMetrics, and with complexity 5 by SonarQube:
Exemptions around switch case
- CC has known issues with the switch statements.
-
They increment the CC by a lot in some cases as compared to IF ELSE statements.
if (n >= 0) { switch(n) { case 0: case 1: printf("zero or one\n"); break; case 2: printf("two\n"); break; case 3: case 4: printf("three or four\n"); break; } } else { printf ("negative\n"); } - Depends on how the CC computation is done
- Some cases are to optimize the switch case code to something better
 Ideally, the switch case should have 7 CC count in total.
Ideally, the switch case should have 7 CC count in total.
Inline Conditional or Ternary operator
switch (age)
{
case < 21:
Console.Write(Under21());
break;
case >= 65:
Console.Write(Over65());
break;
default:
Console.Write(Over21());
break;
}
The complexity of the above function is 4 with the switch case but is 3 with the ternary operator.
Console.Write(age < 21 ? Under21() : age >= 65 ? Over65() : Over21());
Code motion across Functions
func cardinal16ToDegree(dir string) (float64, error) {
switch strings.ToLower(dir) {
case "n":
return 0, nil
case "nne":
return 22.5, nil
case "ne":
return 45, nil
case "ene":
return 67.5, nil
case "e":
return 90, nil
case "ese":
return 112.5, nil
case "se":
return 135, nil
case "sse":
return 157.5, nil
case "s":
return 180, nil
case "ssw":
return 202.5, nil
case "sw":
return 225, nil
case "wsw":
return 247.5, nil
case "w":
return 270, nil
case "wnw":
return 292.5, nil
case "nw":
return 315, nil
case "nnw":
return 337.5, nil
}
return 0, errors.New("could not parse cardinal direction")
}
Can be converted into :
unc Cardinal16ToDegree(dir string) (float64, error) {
switch dir {
case "n":
return 0, nil
case "nne":
return 22.5, nil
case "ne":
return 45, nil
case "ene":
return 67.5, nil
case "e":
return 90, nil
case "ese":
return 112.5, nil
default:
return cardinalHelper(dir)
}
return 0, errors.New("unreachable")
}
func cardinalHelper(dir string) (float64, error) {
switch dir {
case "se":
return 135, nil
case "sse":
return 157.5, nil
case "s":
return 180, nil
case "ssw":
return 202.5, nil
case "sw":
return 225, nil
case "wsw":
return 247.5, nil
case "w":
return 270, nil
case "wnw":
return 292.5, nil
case "nw":
return 315, nil
case "nnw":
return 337.5, nil
}
return 0, errors.New("could not parse cardinal direction")
}
External API usage
Unknown complexity for the tool to detect.
Ruling things with OOPs
It is known that many a times that conditionals are well eradicated in a robust design system of Polymorphism. The design pattern that is commonly used to replace switch-case or if-else conditions is the Strategy Pattern. The Strategy Pattern is a behavioral design pattern that defines a family of algorithms, encapsulates each algorithm, and makes them interchangeable. It allows the client to choose the appropriate algorithm at runtime without modifying the client code.
Shortfalls of Cyclomatic Complexity
Because of its archaic nature, the original paper had some vague ideas on most of the specifics of Cyclomatic Complexity. This has led to confusion and differences in the computation of the final value. Due to the vagueness from the origin of the concept, different tools built for calculating CC , result in having different implementations (sometimes drastic) causing further confusion and differences in usage. Multiple tools have differences in producing CFGs as well.
Adapting this metric to newer language constructs like lamdba or other detailed concepts like multi threading. The metric doesn’t scale very well for such cases. This might hold down the organization from exploring new semantics of the language due to clarity issues on its complexity. Granularity of the check is also very crucial. Decreasing complexity in a function could mean increment of the same metric in other sister function. Such cases are fairly common for the metric being unable to evaluate issues at a holistic level.As we saw in the above section, “cheating” the metric is a common practice performed by the developers. There are ways to break the metric’s check causing it to be an illusion of simplicity but the spaghetti code still exists.
Alternatives
- Cognative Complexity - SonarQube’s new complexity measure that deals with some shortfalls of cyclomatic complexity.
- CERT Secure Coding Standard - Great coding standard for secure coding practices.
- MISRA C:2012 - Guidelines for the use of the C language in critical systems
Personal Opinions
It is a good metric to start evaluating if not already. I consider it more of a sniff test than anything to rigidly adhere to. Usually if my function’s cyclomatic complexity is too high, I know it with or without a sniffer telling me so. However, the things I think we should be careful about is to not exploit the metric so as to dilute it’s intention.
Donald Knuth rightly mentioned the Goodhart’s Law in one of his books. It states that :
What this really means is that with growing dependence on the metrics, the developers might start to optimize the metric itself and loose the sense of the real motive behind the target.
References
- “A Complexity Measure” by T.J. McCabe - https://ieeexplore.ieee.org/document/1702388